Breadth First Search (BFS)

Many application of graph requires a structure based system to determine the vertices and edges of a graph G. That is called a graph traversal, which means visiting all the nodes of the graph. There are two graph traversal methods

-a) Breadth First Search (BFS)

-b) Depth First Search (DFS)

Today i will discuss about Breadth First Search. Given an input graph G = (V, E) and a source vertex S, from where the searching begins. The Breadth first search(BFS) systematically traverse the edges of G to explore every vertex that is reachable from the source vertex S. Then we examine all the vertices neighbour to source vertex S. Then we traverse all the neighbours of the neighbours of source vertex S and so on. A queue is used to keep track of the progress of traversing the neighbour nodes.

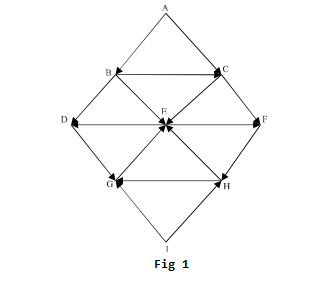
Now,I will discuss Breadth First Search with an example.Because it will be more easier approach to understand BFS. Consider the following graph in Fig 1 and it’s corresponding adjacency list (Fig 2).

   
           

Suppose  the source vertex is A . Then following steps will illustrate the Breadth First Search (BFS).

Step 1: Initially we push A (the given source vertex) to the queue.

Step 2: Pop (remove) the front element A from the queue (by incrementing front =front +1) and display it. Then push (add) the neighbouring vertices of A to the queue, (by incrementing Rear = Rear +1) if it is not in queue.

Step 3: Pop the front element B from the queue and display it. Then add the

neighbouring vertices of B to the queue, if it is not in queue.

One of the neighbouring element C of B is present in the queue, So C is not added to queue.

Step 4: Remove (pop) the front element C and display it. Add the neighbouring vertices of C,if it is not present in queue.

 One of the neighbouring elements E of C is present in the queue. So E is not added.

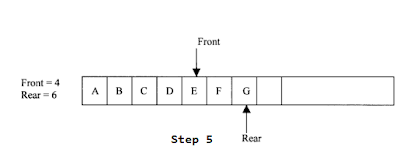
Step 5: Remove the front element D, and add the neighbouring vertex if it is not present in queue.

Step 6 : Again repeat the process (until Front > Rear).That is remove the front element E of the queue and add it to the neighbouring vertex if it is not present in the queue.

So A, B, C, D, E, F, G, H is the Breadth First Search(BFS)  traversal of the  given graph in Fig. 1. I hope now you have understood the BFS traversal method. So now have a look on the formal BFS algorithm given below :

ALGORITHM

1. Input the vertices of the graph and its edges G = (V, E)

2. Input the source vertex and assign it to the variable S.

3. Add or push the source vertex to the queue.

4. Repeat the steps 5 and 6 until the queue is empty (i.e., front > rear)

5. Pop the front element of the queue and display it as visited.

6. Push the vertices, which is neighbor to just, popped element, if it is not in       the queue and displayed (i.e., not visited).

7. Exit.

If you have any question regarding Breadth First Search,please comment below in the comment box.I shall try my best to answer your queries...soon i will be posting the Depth First Search(DFS) traversal method .keep visiting regularly for more updates...:)

------------------------------------------------------------------------------------------------------------

REGARDS

Shankha Jana